1.6 树-基本概念
树的定义
树是一种数据结构,它是n(n>=0)个节点的有限集。n=0时称为空树。n>0时,有限集的元素构成一个具有层次感的数据结构。
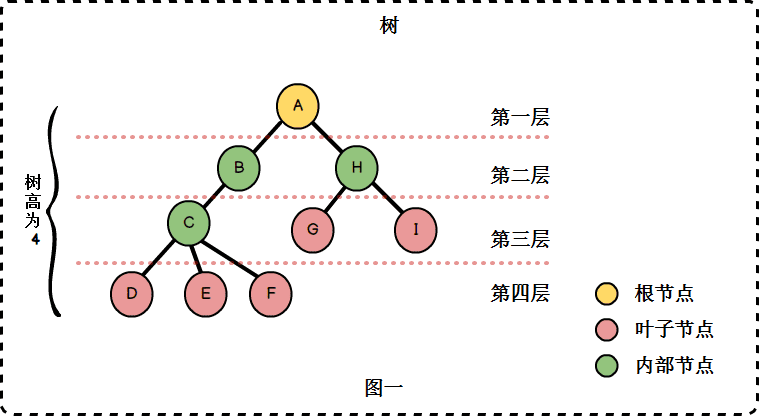
区别于线性表一对一的元素关系,树中的节点是一对多的关系。树具有以下特点:
- n>0时,根节点是唯一的,不可能存在多个根节点。每个节点有零个至多个子节点;
- 除了根节点外,每个节点有且仅有一个父节点。根节点没有父节点。
基本概念
树是一种重要的数据结构,具有许多基本概念,以下是其中一些:
节点(Node):树的基本构建单元,它可以包含一个数据元素,也可以包含多个数据元素,这取决于树的类型。
根节点(Root Node):树的顶部节点,它是树的唯一起始点,所有其他节点都直接或间接地从根节点派生。
父节点(Parent Node):一个节点的直接上级节点。
子节点(Child Node):一个节点的直接下级节点。
叶子节点(Leaf Node):没有子节点的节点,它们位于树的末端。
子树(Subtree):树中任意节点及其后代节点组成的结构,这也是树的基本组成部分。
深度(Depth):树中某个节点到根节点的唯一路径的长度。根节点的深度为0,其子节点的深度为1,以此类推。
高度(Height):树中节点的最大深度。树的高度取决于最远的叶子节点到根节点的路径的长度。
父节点与子节点之间的关系:父节点到子节点的连接,这种连接定义了树的结构。
兄弟节点(Sibling Node):拥有同一个父节点的节点互为兄弟节点。
祖先节点(Ancestor Node):某个节点的所有直接或间接上级节点。
后代节点(Descendant Node):某个节点的所有直接或间接下级节点。
有序树与无序树:有序树中节点之间的子节点有顺序,而无序树中节点之间的子节点没有特定的顺序。
二叉树(Binary Tree):每个节点最多有两个子节点的树。
平衡树(Balanced Tree):树中任意节点的左右子树的高度差不超过1的二叉树。
满二叉树(Full Binary Tree):除了叶子节点外,每个节点都有两个子节点的二叉树。
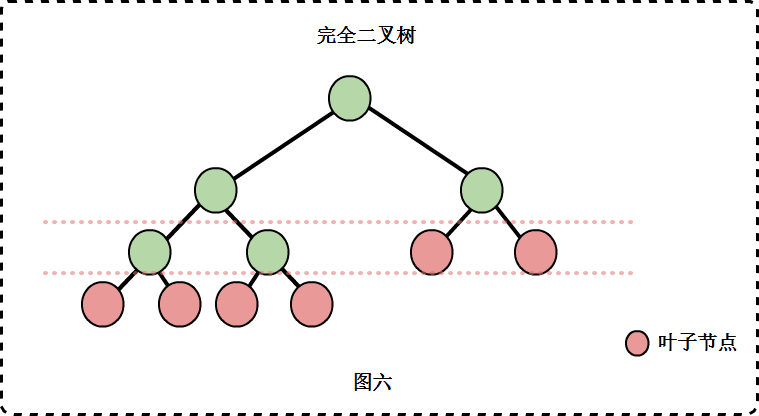
完全二叉树(Complete Binary Tree):除了最后一层外,所有层的节点都被填满,并且最后一层的节点都靠左排列的二叉树。
树的分类
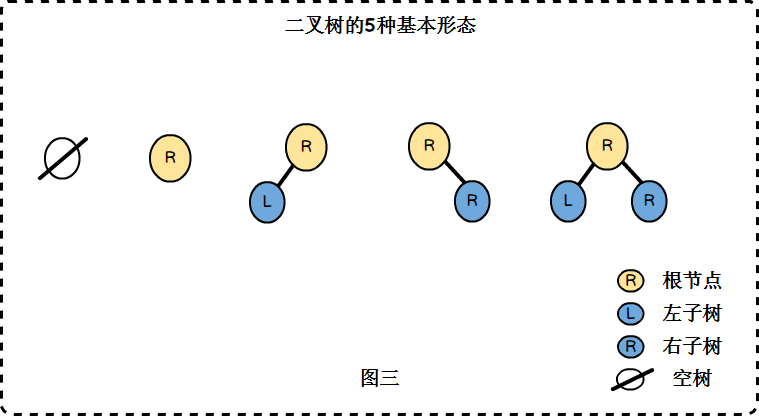
二叉树
最多有两棵子树的树被称为二叉树
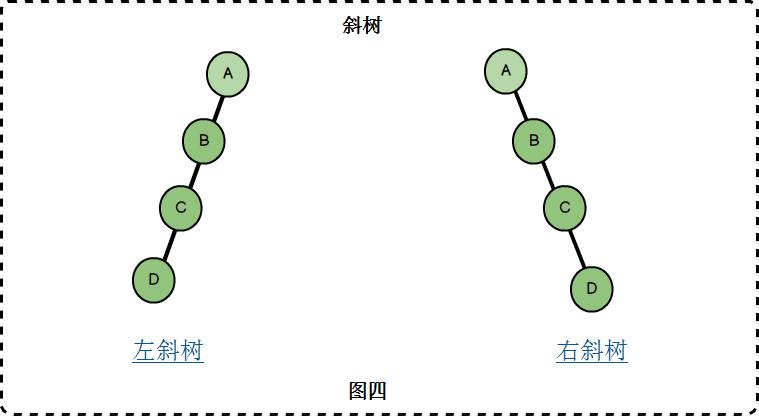
斜树
所有节点都只有左子树的二叉树叫做左斜树,所有节点都只有右子树的二叉树叫做右斜树。
满二叉树
二叉树中所有非叶子结点的度都是2,且叶子结点都在同一层次上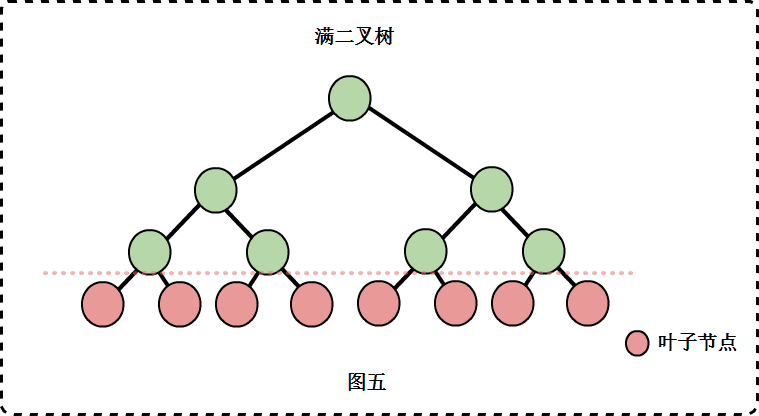
完全二叉树
如果一个二叉树与满二叉树前m个节点的结构相同,这样的二叉树被称为完全二叉树